题目

奇妙变换

解题思路（直接按定义实现递归）

核心观察：题目定义就是递归结构

函数 f(x) 的定义天然分为两种情况：

• 当 x 小于等于 10 时：直接返回 x * (x - 1)
• 当 x 大于 10 时：返回 2 * x * f(x - 6)

这种“自己调用自己”的形式，就是递归的典型场景。对于刚学递归的同学，这道题的目的就是让你照着数学定义写代码，不需要任何转换或优化。

为什么不用优化也能 AC？

虽然看起来可能担心递归深度太大，但实际上：

• 每次递归 x 减少 6，所以递归层数大约是 n / 6
• 题目在 OJ 上的数据较弱，n 不会大到导致栈溢出
• 本题重点是理解递归的基本写法，而不是性能优化

口诀：定义什么样，代码就怎么写

取模处理的注意事项

结果要对 998244353 取模。虽然理论上可以在最后取模，但为了防止中间结果超出 long 范围，在基础情况就进行取模更安全。由于每次只做几次乘法，使用 long 类型足以应对中间结果。

参考代码

import java.util.Scanner;

public class Main {
    static int MOD = 998244353;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        long x = sc.nextLong();
        System.out.println(f(x) % MOD);
    }

    private static long f(long x) {
        // 基础情况: 当 x <= 10 时, 直接计算 x * (x - 1) 并取模
        if (x <= 10) {
            return x * (x - 1) % MOD;
        }
        // 递归情况: f(x) = 2 * x * f(x - 6)
        // 对 f(x - 6) 的结果取模, 避免中间值过大
        return 2 * x * (f(x - 6) % MOD);
    }
}

鸡哥的魔法石

解题思路（递归实现两种写法对比）

核心观察：模拟吸收过程并计数

魔法石每次将当前数字减去其各位数字之和，直到变为 0。题目明确说明：当数字为 0 时，也算作一次吸收。例如 24 的过程是：24 → 18 → 9 → 0，共 4 次（含最后的 0）。

关键性质：递归天然匹配“重复操作”

每一步操作结构相同：计算数位和、减去、继续处理新值。这种“自己调用自己”的结构非常适合用递归来表达。

两种递归风格对比

• 全局变量写法：函数不返回结果，靠副作用（修改全局 cnt）记录次数。适合初学者理解“执行了多少次”，但状态耦合，不易复用。
• 返回值写法：函数 f(n) 直接表示“从 n 到 0 需要多少次”，语义清晰、无副作用，是更规范的递归写法。

💡 推荐“有明确返回值”的递归，这是更规范、可测试、可组合的编程方式

参考代码

方法一：使用全局变量统计次数

import java.util.Scanner;

public class Main {
    static int cnt; // 全局计数器: 记录吸收次数

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        f(n); // 启动递归, 副作用修改 cnt
        System.out.println(cnt);
    }

    /**
     * 递归执行吸收过程: 每进入一次就计数一次
     * @param n 当前剩余能量值
     */
    private static void f(int n) {
        cnt++; // 本次吸收计入次数
        if (n == 0) {
            return; // 终止条件: 已到 0, 不再继续
        }
        int sum = getDigitSum(n); // 计算当前数字的各位数字之和
        f(n - sum); // 递归处理下一次吸收后的值
    }

    /**
     * 计算一个正整数的各位数字之和
     * @param n 输入的数字
     * @return 各位数字相加的结果
     */
    private static int getDigitSum(int n) {
        int sum = 0;
        while (n > 0) {
            sum += n % 10; // 取个位
            n /= 10;       // 去掉个位
        }
        return sum;
    }
}

方法二：递归函数直接返回吸收次数

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int cnt = f(n); // 直接获取从 n 到 0 的总吸收次数
        System.out.println(cnt);
    }

    /**
     * 返回将数字 n 吸收到 0 所需的总次数
     * @param n 当前能量值
     * @return 吸收次数
     */
    private static int f(int n) {
        if (n == 0) {
            return 1; // 0 也算一次吸收: 这是最后一次
        }
        int sum = getDigitSum(n); // 获取当前数位和
        return 1 + f(n - sum); // 本次吸收(1次) + 后续吸收次数
    }

    /**
     * 计算一个正整数的各位数字之和
     * @param n 输入的数字
     * @return 各位数字相加的结果
     */
    private static int getDigitSum(int n) {
        int sum = 0;
        while (n > 0) {
            sum += n % 10; // 累加个位
            n /= 10;       // 移除个位
        }
        return sum;
    }
}

串变换

解题思路(回溯枚举操作子集)

核心观察：操作可选且顺序任意，本质是枚举子集

题目允许我们从 k 个操作中任选若干个，以任意顺序执行一次。由于 k ≤ 7，总子集数最多为 ​2^7 = 128，完全可以暴力枚举所有可能的操作组合。

关键性质：回溯天然适合“选或不选”问题

每个操作只有两种状态：使用 或 不使用。这构成一棵深度为 k 的二叉搜索树（实际实现中用 for 循环横向遍历所有未使用操作，等价于枚举子集）。

• 树的节点：表示执行了某几个操作后的字符串状态
• 搜索目标：任意一个节点（不一定是叶子）满足 S == T 即可

💡 注意：不需要执行完所有操作，只要中途达到目标就成功，因此要在每次递归入口检查是否匹配。

回溯三要素精准对应

• 参数：当前字符串状态 s、操作数组 ops、使用标记 used
• 终止条件：发现 s == t 时立即设 found = true 并返回
• 遍历过程：对每个未使用的操作，尝试执行 → 递归 → 回溯恢复原状

参考代码

import java.util.Scanner;

public class Main {
    // 全局标志: 记录是否找到可行方案
    static boolean found = false;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        String sStr = sc.next();
        String tStr = sc.next();
        // 将字符串转为整数数组: 方便进行数字运算和交换
        int[] s = new int[n];
        int[] t = new int[n];
        for (int i = 0; i < n; i++) {
            s[i] = sStr.charAt(i) - '0';
            t[i] = tStr.charAt(i) - '0';
        }
        // 读取操作数量k
        int k = sc.nextInt();
        // 存储所有操作: ops[i][0]为操作类型, ops[i][1]和ops[i][2]为参数
        int[][] ops = new int[k][3];
        for (int i = 0; i < k; i++) {
            ops[i][0] = sc.nextInt();
            ops[i][1] = sc.nextInt();
            ops[i][2] = sc.nextInt();
        }
        // used[i]标记第i个操作是否已被使用
        boolean[] used = new boolean[k];
        // 启动回溯搜索
        dfs(ops, s, t, used);
        // 输出结果
        System.out.println(found ? "Yes" : "No");
    }

    /**
     * 回溯搜索函数: 尝试所有未使用操作的组合
     * @param ops 所有操作的列表
     * @param s 当前字符串状态(会动态修改)
     * @param t 目标字符串状态(只读)
     * @param used 操作使用标记数组
     */
    private static void dfs(int[][] ops, int[] s, int[] t, boolean[] used) {
        // 剪枝: 如果已经找到解, 直接返回
        if (found) {
            return;
        }
        // 检查当前状态是否匹配目标: 在每个节点都检查(不要求执行完所有操作)
        if (isSame(s, t)) {
            found = true;
            return;
        }
        // 遍历所有操作: 横向遍历(树的宽度)
        for (int i = 0; i < ops.length; i++) {
            // 跳过已使用的操作
            if (used[i]) {
                continue;
            }
            int op = ops[i][0]; // 操作类型
            int x = ops[i][1];  // 第一个参数
            int v = ops[i][2];  // 第二个参数(操作1中是增量, 操作2中是y)
            // 保存现场: 用于后续回溯
            int originalX = s[x];
            int originalY = s[v]; // 仅交换操作需要保存y

            // 执行操作
            if (op == 1) {
                // 类型1: S[x] = (S[x] + v) mod 10
                s[x] = (s[x] + v) % 10;
            } else {
                // 类型2: 交换 S[x] 和 S[v]
                int temp = s[x];
                s[x] = s[v];
                s[v] = temp;
            }

            // 标记操作已使用
            used[i] = true;
            // 纵向递归: 进入下一层(树的深度)
            dfs(ops, s, t, used);
            // 回溯: 恢复现场
            used[i] = false;
            if (op == 1) {
                // 恢复S[x]的原始值
                s[x] = originalX;
            } else {
                // 恢复交换: 再次交换即可
                s[x] = originalX;
                s[v] = originalY;
            }
        }
    }

    /**
     * 辅助函数: 判断两个数组是否完全相等
     * @param s 当前字符串数组
     * @param t 目标字符串数组
     * @return 如果所有位置字符相同返回true, 否则false
     */
    private static boolean isSame(int[] s, int[] t) {
        for (int i = 0; i < s.length; i++) {
            if (s[i] != t[i]) {
                return false;
            }
        }
        return true;
    }
}

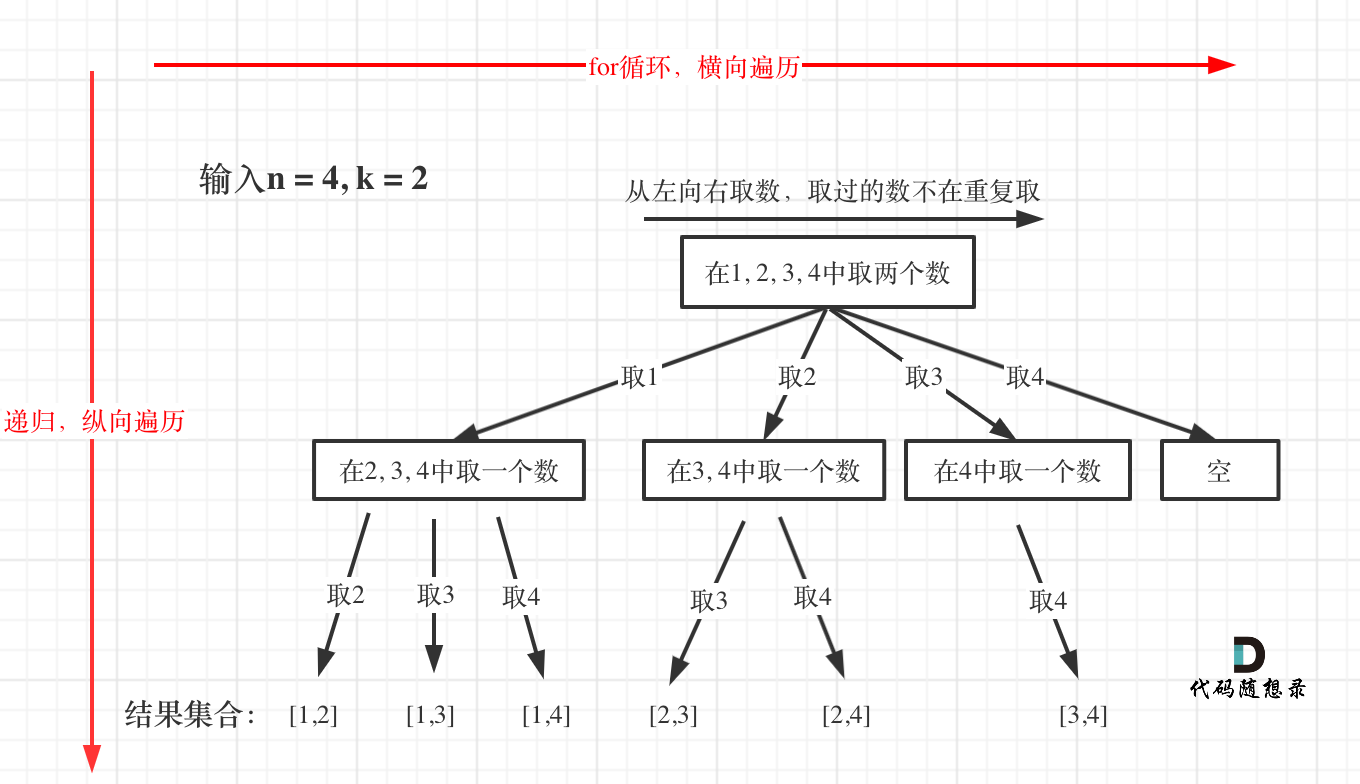
通用回溯解题框架（适用于所有子集/排列类问题）

回溯算法的本质是在隐式树上进行深度优先搜索，其核心步骤可归纳为以下三部曲：

1. 确定搜索空间与状态表示
   • 每一层代表“是否选择第 i 个元素”
   • 状态包括：当前路径（已选操作）、原始数据副本、辅助标记等
2. 设计回溯函数三要素
   • 参数：传递当前状态（如数组、标记位）
   • 终止条件：到达目标状态或无法继续扩展
   • 遍历逻辑：横向 for 循环枚举本层所有选择，纵向递归深入下一层
3. 实现“修改 → 递归 → 回溯”原子操作
   • 修改：应用当前选择（如执行操作、标记使用）
   • 递归：进入下一层搜索
   • 回溯：撤销修改（恢复现场），保证后续分支不受影响

📌 “for 横向选，递归纵向走，做完要回退，状态不能丢”

宝塔

解题思路（回溯+剪枝求解唯一解）

核心观察：规则等价于带额外约束的拉丁方

题目要求每行每列数字 1~N 不重复（类似数独），同时四个方向的“可见塔数”必须匹配边界提示。可见塔数定义为：从某方向看，高度严格递增序列的长度（即只能看到比前面所有塔都高的塔）。

关键性质：回溯天然适合约束满足问题

• 状态空间：5×5 网格，每个格子填 1~5，总状态 ​5^{25} 极大
• 剪枝策略：
  1. 行/列重复剪枝：填数时立即检查行列冲突（isRepeat）
  2. 延迟验证：仅当网格填满后才验证四方向可见数（checkFourDir）
• 唯一解保证：题目说明答案唯一，找到即终止

通用回溯优化技巧

• 逐格填充：按行优先顺序遍历空位，避免重复搜索
• 早停机制：一旦某格无法填入任何数字，立即回溯
• 最终验证：将复杂约束（四方向）留到最后检查，减少中间计算开销

💡 重点：对于多约束问题，应区分“高频剪枝条件”（行列不重复）和“低频验证条件”（四方向可见数），前者用于实时剪枝，后者用于终态验证。

参考代码

public class Main {
    // 棋盘大小
    static int n = 5;
    // 四周的可见塔数提示: left[i]表示第i行左侧可见数
    static int[] left = {2, 2, 3, 2, 1};
    static int[] right = {3, 3, 1, 2, 4};
    static int[] up = {2, 2, 1, 3, 3};
    static int[] down = {1, 4, 2, 2, 3};
    // 棋盘状态: 0表示未填充
    static int[][] grid = new int[5][5];

    public static void main(String[] args) {
        // 启动回溯搜索
        dfs(grid);
        // 按行优先顺序输出结果
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                System.out.print(grid[i][j]);
            }
        }
    }

    /**
     * 回溯搜索函数: 尝试填充棋盘
     *
     * @param grid 当前棋盘状态
     * @return 是否找到合法解
     */
    private static boolean dfs(int[][] grid) {
        // 遍历每个格子寻找空位
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                // 跳过已填充的格子
                if (grid[i][j] != 0) {
                    continue;
                }
                // 尝试填入1~n的每个数字
                for (int num = 1; num <= n; num++) {
                    // 剪枝: 检查行列是否重复
                    if (isRepeat(grid, i, j, num)) {
                        continue;
                    }
                    // 填入数字
                    grid[i][j] = num;
                    // 递归搜索后续格子
                    if (dfs(grid)) {
                        return true; // 找到解立即返回
                    }
                    // 回溯: 恢复空位
                    grid[i][j] = 0;
                }
                // 当前格子所有数字都尝试失败, 回溯
                return false;
            }
        }
        // 棋盘已填满, 验证四方向可见塔数
        if (!checkFourDir(grid)) {
            return false; // 不符合边界条件
        }
        return true; // 找到唯一解
    }

    /**
     * 检查在(i,j)位置填入num是否导致行列重复
     *
     * @param grid 当前棋盘
     * @param x    行索引
     * @param y    列索引
     * @param num  待填数字
     * @return 是否存在重复
     */
    private static boolean isRepeat(int[][] grid, int x, int y, int num) {
        // 检查行重复
        for (int j = 0; j < n; j++) {
            if (grid[x][j] == num) {
                return true;
            }
        }
        // 检查列重复
        for (int i = 0; i < n; i++) {
            if (grid[i][y] == num) {
                return true;
            }
        }
        return false;
    }

    /**
     * 验证棋盘四方向可见塔数是否符合提示
     *
     * @param grid 完整填充的棋盘
     * @return 是否满足所有边界条件
     */
    private static boolean checkFourDir(int[][] grid) {
        // 检查左右方向(按行)
        for (int i = 0; i < n; i++) {
            // 左侧可见数
            int max = 0, cnt = 0;
            for (int j = 0; j < n; j++) {
                if (grid[i][j] > max) {
                    max = grid[i][j];
                    cnt++;
                }
            }
            if (cnt != left[i]) return false;

            // 右侧可见数
            max = 0;
            cnt = 0;
            for (int j = n - 1; j >= 0; j--) {
                if (grid[i][j] > max) {
                    max = grid[i][j];
                    cnt++;
                }
            }
            if (cnt != right[i]) return false;
        }

        // 检查上下方向(按列)
        for (int i = 0; i < n; i++) {
            // 上侧可见数
            int max = 0, ans = 0;
            for (int j = 0; j < n; j++) {
                if (grid[j][i] > max) {
                    max = grid[j][i];
                    ans++;
                }
            }
            if (ans != up[i]) return false;

            // 下侧可见数
            max = 0;
            ans = 0;
            for (int j = n - 1; j >= 0; j--) {
                if (grid[j][i] > max) {
                    max = grid[j][i];
                    ans++;
                }
            }
            if (ans != down[i]) return false;
        }
        return true;
    }
}

与或异或

解题思路（暴力枚举+递推验证）

核心观察：结构固定，仅运算符可变

题目给出一个5层金字塔结构的逻辑电路：

• 第 0 层（输入层）：5 个已知比特 [1, 0, 1, 0, 1]
• 第 i 层（i ≥ 1）：有 5 - i 个节点，每个节点由上一层相邻两个节点通过某个二元逻辑门计算得出
• 总共需要 10 个门电路（4+3+2+1=10），每个门可以是 OR（|）、XOR（^）、AND（&） 中的一种

目标：统计所有 10 个门的类型组合 中，使得最终输出（第 4 层唯一节点）为 1 的方案总数。

关键性质：状态空间小，适合暴力枚举

• 每个门有 3 种选择 → 总组合数为 ​3^{10} = 59049
• 对每种组合，只需 O(n²) = O(25) 时间模拟计算结果
• 总计算量 ≈ 150 万次操作，完全可在瞬间完成

算法设计：回溯枚举 + 逐层递推

1. 枚举阶段：用 DFS 枚举 ops[0..9]，每个位置取值 1/2/3 分别代表 |，^ ，&
2. 验证阶段：当 10 个运算符确定后，从第 1 层开始逐层计算 grid[i][j]
   • grid[i][j] = apply_op(grid[i-1][j], grid[i-1][j+1], ops[index])
3. 计数：若 grid[4][0] == 1，则答案加 1

💡 优化提示：虽然可以边枚举边剪枝（如提前发现某层全 0 且后续无法变 1），但本题规模极小，直接暴力更简洁可靠。

---

参考代码

public class Main {
    static int n = 5;
    static int[] ops = new int[10]; // 存储10个门的类型: 1=|, 2=^, 3=&
    static int[][] grid = new int[n][n];

    public static void main(String[] args) {
        // 初始化输入层
        grid[0][0] = 1;
        grid[0][1] = 0;
        grid[0][2] = 1;
        grid[0][3] = 0;
        grid[0][4] = 1;
        // 枚举所有运算符组合并计数
        int result = dfs(0);
        System.out.println(result);
    }

    /**
     * 回溯枚举第 cnt 个门的类型 (共10个)
     * @param cnt 当前正在枚举的门索引 (0 ~ 9)
     * @return 满足最终输出为1的方案数
     */
    private static int dfs(int cnt) {
        // 所有10个门已确定，开始计算输出
        if (cnt == 10) {
            int index = 0;
            // 从第2层到第5层逐层计算
            for (int i = 1; i < n; i++) {
                for (int j = 0; j < n - i; j++) {
                    int a = grid[i - 1][j];
                    int b = grid[i - 1][j + 1];
                    int op = ops[index++];
                    if (op == 1) {
                        grid[i][j] = a | b;      // OR
                    } else if (op == 2) {
                        grid[i][j] = a ^ b;      // XOR
                    } else { // op == 3
                        grid[i][j] = a & b;      // AND
                    }
                }
            }
            // 检查最终输出是否为1
            return grid[4][0] == 1 ? 1 : 0;
        }

        // 尝试三种门类型
        int total = 0;
        for (int opType = 1; opType <= 3; opType++) {
            ops[cnt] = opType;
            total += dfs(cnt + 1);
            // ops[cnt] = 0; // 非必需，因下轮会被覆盖
        }
        return total;
    }
}

五子棋对弈

解题思路（回溯枚举+胜负剪枝）

核心观察：平局 = 满盘 + 无五连

题目要求统计所有 25格全填满 且 没有任何一方形成五子连线 的合法棋局数量。由于白棋先手，总步数为25（奇数），因此白棋下13子、黑棋下12子。

关键性质：回溯天然适合“逐格填子 + 实时胜负检测”

• 棋盘规模小（5×5），总状态虽多但可通过剪枝大幅压缩
• 胜负判定只需在落子后检查：因为五连只能由最新落子促成
• 无需记录used数组：用一维位置 pos（0~24）线性遍历，自动保证不重复填子

剪枝策略：提前终止非法分支

1. 数量限制：白棋最多13个，黑棋最多12个

2. 胜负剪枝：若某方落子后立即形成五连，则该分支无效，直接跳过

   • 使用 isWin(x, y, player) 检查以 (x,y) 为中心的四个方向（横、竖、主对角、副对角）

• 每个方向双向扩展，累计连续同色子数 ≥5 即判胜

---

参考代码

public class Main {
    static int n = 5;
    static int[][] grid = new int[n][n]; // 0: 空, 1: 白棋, 2: 黑棋

    public static void main(String[] args) {
        // 从第0个位置开始，白棋0颗，黑棋0颗
        int result = dfs(0, 0, 0);
        System.out.println(result);
    }

    /**
     * 回溯枚举所有合法平局局面
     * @param pos 当前要填的位置（0 ~ 24）
     * @param white 已放置的白棋数量
     * @param black 已放置的黑棋数量
     * @return 合法平局局面总数
     */
    private static int dfs(int pos, int white, int black) {
        // 所有格子已填满，达成平局条件
        if (pos == n * n) {
            return 1;
        }
        int x = pos / n; // 行坐标
        int y = pos % n; // 列坐标
        int total = 0;

        // 尝试放白棋（1）：白棋最多13颗，且不能导致胜利
        if (white < 13 && !) {
            grid[x][y] = 1;
            total += dfs(pos + 1, white + 1, black);
            grid[x][y] = 0; // 回溯
        }

        // 尝试放黑棋（2）：黑棋最多12颗，且不能导致胜利
        if (black < 12 && !isWin(x, y, 2)) {
            grid[x][y] = 2;
            total += dfs(pos + 1, white, black + 1);
            grid[x][y] = 0; // 回溯
        }

        return total;
    }

    // 四个检测方向：右、右下、下、左下
    static int[][] dirs = {{0, 1}, {1, 1}, {1, 0}, {1, -1}};

    /**
     * 判断在(x, y)落子player后是否形成五子连珠
     * @param x 落子行
     * @param y 落子列
     * @param player 棋子颜色（1: 白, 2: 黑）
     * @return 是否获胜
     */
    private static boolean isWin(int x, int y, int player) {
        for (int[] dir : dirs) {
            int dx = dir[0];
            int dy = dir[1];
            int count = 1; // 当前落子算1个

            // 正方向延伸（如向右）
            for (int i = 1; i < 5; i++) {
                int nx = x + i * dx;
                int ny = y + i * dy;
                if (nx < 0 || nx >= n || ny < 0 || ny >= n || grid[nx][ny] != player) {
                    break;
                }
                count++;
            }

            // 反方向延伸（如向左）
            for (int i = 1; i < 5; i++) {
                int nx = x - i * dx;
                int ny = y - i * dy;
                if (nx < 0 || nx >= n || ny < 0 || ny >= n || grid[nx][ny] != player) {
                    break;
                }
                count++;
            }

            // 任一方向连续≥5即获胜
            if (count >= 5) {
                return true;
            }
        }
        return false;
    }
}